Problemas MLLS(Multilevel-lot sizing)

Los problemas MLLS (Multilevel-lot sizing) hacen parte de los problemas clásicos de MRP(Planeación de requerimientos de los materiales) que básicamente están definidos para establecer el articulo adecuado, en la cantidad adecuada y en el momento adecuado(Joseph Orilcky 1975).

A su vez esta puede ser definida  como un grupo de técnicas que utiliza los datos de inventario, las estructuras de productos, y los planes maestros de producción para determinar los materiales requeridos. La determinación del tamaño de lotes multinivel es un problema al cual se enfrentan las empresas a menudo organizando sus planes de producción. Su objetivo principal es determinar el tamaño óptimo del lote y de inventario para minimizar  el costo (de producción, inventarios, costo de nuevo el pedido, y otros). Este problema también puede ser clasificado en diferentes categorías de acuerdo a las estructuras de los productos (sistema de un solo nivel, montaje en serie, los sistemas generales ...) y según las estructuras de la capacidad (sin capacidad determinada, capacitados único recurso, y capacitado a varios recursos).

Aunque los modelos con capacidad determinada son mejores, en la práctica los modelos sin límite de tamaño son  utilizados más frecuentemente debido a que la implementación de los anteriores requiere muchos datos que las empresas no son capaces o simplemente no quieren recoger.

El propósito del artículo es presentar la solución al problema de determinación del tamaño del lote multinivel por medio de un algoritmo de enjambre de partículas.

Solución de problemas MLLS

Para la solución de estos problemas generalmente se usaban métodos heurísticos (basados en la experiencia), pero con el avance de la computación (EMC) se comenzó a usar herramientas tales como la simulación y el uso de algoritmos tales como el de enjambre de partículas (Particle Swarm Optimization(PSO)), el cual fue desarrollado por Kennedy y Eberhart en 1995, como un método de cálculo que optimiza un problema de forma iterativa tratando de mejorar una solución de candidatos en relación con a una determinada medida de la calidad. El algoritmo de enjambre de partículas optimiza un problema teniendo una población de soluciones candidatas, aquí llamado partículas, y moviendo estas partículas en torno al espacio búsqueda a través de unas fórmulas matemáticas simples sobre la velocidad y la posición de la partícula.

El movimiento de cada partícula es influenciada por su mejor posición local conocida y se orienta también hacia las mejores posiciones conocidas en el espacio de búsqueda, y son actualizadas como una mejor posición cuando se encuentran con otras partículas. Esto mueve el enjambre hacia las mejores soluciones. La intención original de PSO fue simular gráficamente la coreografía elegante, pero impredecible de una bandada de aves, pero ahora se está aplicando en diferentes campos de la investigación de operaciones.

Para la solución de estos modelos se debe establecer el modelo matemático a utilizar, el esquema adecuado para el PSO y por ultimo a través de la simulación llevar el problema MLLS a su nueva posible solución.

Modelo Matemático

Estos problemas poseen tres estructuras de producto (1) estructura de montaje, (2) estructura arborescente (Ramificación)  y la (3) estructura general. Este modelo matemático representa un conjunto de nodos donde cada nodo corresponde a un artículo y el limite (i,j) entre el nodo i y el nodo j quiere decir que el articulo i es directamente requerido para montar el articulo j. Donde      R^-1(i) y R(i) para representar al inmediato predecesor y al sucesor del nodo i, mientras que R´ ^-1(i) denota a todos los predecesores del nodo i. Un ejemplo según la imagen R^-1(1)={2,3} , R´ ^-1(1)={2,3,4,5} para el nodo 1 y para el nodo 4, R-1(4)={2,3} , R´ -1(4)={1,2,3}.

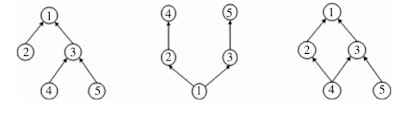Tipos de Estructuras

Se asume que la estructura de producción solo incluye un solo producto final, los costos variables y los costos de producción no son  tomados en cuenta, el lead time= 0 (tiempo de reorden del pedido), el inventario inicial (I_i,0= 0  ∀ i). los problemas de MLLS son programas enteros mixtos, y para su modelación se usara la siguiente denotación:

·         i índice del articulo

·         C_i,j Cantidad de articulo i para producir un artículo j

·         H_i Costo de tener en inventario para articulo i

·         K_i Costo de puesta en marcha del articulo i

·         L_i Lead Time para montar, comprar o manufacturar el articulo i

·         L_i.t Nivel de inventario i al final del periodo t

·         A_i,t Variable binaria para capturar el costo de puesta en marcha del articulo i entregada en el tiempo t

·         D_i,t Requerimientos para el articulo i en el tiempo j

·         P_i,t  Cantidades de producción/reposición para i en el tiempo t

·         M un número muy grande

·         N  El número total de artículos

·         T La longitud del horizonte de producción

La matriz de decisión:

Función Objetivo

Restricciones

La función objetivo es la suma de los costos de puesta en marcha y de mantenimiento de inventarios para todos los artículos dentro del horizonte de producción. La primera restricción establece el balance entre la ecuación de producción y la de reposición del inventario y la demanda. La segunda restricción proporciona la fórmula para calcular la demanda interna. La tercera restricción garantiza que el tamaño de la reposición de cierto periodo depende de la decisión de puesta en marcha de periodos anteriores. La cuarta restricción garantiza que el costo de puesta en marcha tendrá valor cuando un lote sea comprado o producido y por último que los atrasos no son permitidos y que la producción es mayor o igual que cero.

Esquema para el algoritmo PSO

Como previamente se había nombrado el algoritmo PSO es capaz de encontrar la solución óptima de un conjunto de partículas (candidatas a solución) a través de fórmulas simples de velocidad y aceleración para encontrar la posible ubicación de la partícula es así que la elección de su esquema se define en la elección de la ecuación que definirá el modelo de la simulación:

 Velocidad(V)

·         Velocidad+Velocidad

·         Velocidad-Velocidad

·         Posicion+Velocidad

·         Pocision-Posicion

·         Coeficiente*Velocidad

Para más información sobre la elección del esquema a utilizar buscar  las siguientes referencias:

Pseudocodigo del algoritmo PSO

Marcos experimentales y  simulación

Luego de tener el modelo matemático listo y el esquema del algoritmo PSO se va a la obtención de resultados por medio de la simulación aqui un ejemplo: